Death Star Firepower

Written: 1998.10.31
Last Revised: 1999.01.24

Exactly how powerful is the Death Star? With a little bit of physics and a little bit of math, we can determine just how much power you would need in order to blow up a planet.

Let's start with what we know. The Death Star is capable of destroying any inhabitable planet in the galaxy, blasting it into rubble and hurling the rubble into space at fantastic speeds. This is one of the central defining events of the Star Wars trilogy. In fact, not only did we see the planet Alderaan destroyed in a cataclysmic explosion, but we also saw Han Solo arrive a few minutes later, only to see nothing but a light "meteor shower." This indicates that not only was the planet destroyed, but most of its mass was already dispersed far away from its original location.

	Oneof the tributary beams of the Death Star superlaser (click to enlarge)
	The superlaser beam lances out toward the planet (click to enlarge)

How much energy did it take to destroy Alderaan? In order to answer this question, we must first address a few myths:

1. "A planet can be destroyed by breaking it up into pieces, without having to blow it apart completely". This fails to account for the forces of gravity. Even if you created a hypothetical weapon that sliced a planet cleanly in half, the planet's gravity would immediately slam the two halves back together again. Everyone on the surface would undoubtedly die, but the planet itself would be intact.

2. "A planet can be destroyed by vaporizing or melting it alone". Contrary to popular belief, vapourization alone will not totally destroy the planet, although it will render it quite useless for habitation. Much of a planet's mass is in liquid form already, and even if it were all vaporized, it would only turn into a gas planet. This gas planet would eventually cool and solidify again.

3. "Alderaan might have been a very tiny planet, so it would have been very easy to destroy". There is a fairly narrow range of planet types which can support human life. A human-habitable planet must have sufficient gravity to have retained an atmosphere after its formation, so Alderaan simply could not have been an extremely small planet. Furthermore, the Death Star has been explicitly described to be capable of destroying any inhabited planet.

So if we can't use melting energy or vaporization energy, how do we determine the energy requirement to destroy a planet? The answer, in one word, is gravity. If you wish to destroy a planet, you must scatter its mass so quickly that the forces of gravity cannot reverse the expansion process. In other words, you must accelerate the planet's entire mass to escape velocity. Another way of saying this is that you must bring the planet's gravitational potential energy state up to zero. The concepts of gravititational potential energy and escape velocity are both discussed in the science page. Using those concepts, the energy requirement for blasting a planet apart can be calculated.

Alderaan's fiery death

In this document, we will discuss three different methods for evaluating the energy requirement for scattering a planetary mass at sufficient velocity to overcome gravitational attraction. We will evaluate two of those methods.

Method 1: Surface Escape Velocity

The surface escape velocity for an Earth-like planet is roughly 11.2 km/s. How did we determine this? We used Newton's formula for gravitational potential energy, which is:

In this formula, G is the gravitational constant, which is 6.67E-11 m³/(s²·kg). The two mass figures m1 and m2 are the masses of the two bodies being gravitationally attracted toward one another, and the radius r is the distance between the two bodies. If we substitute m1 = 5.97E24kg for the Earth's mass and r = 6.37E6m into the above equation, we can easily rearrange the equation to determine that the escape velocity for any mass m2 at the surface of the planet is roughly 11.2 km/s.

Therefore, the most straightfoward method of determining the energy requirement for planetary destruction is to simply substitute the planet's mass and surface escape velocity into the classical kinetic energy equation as follows:

KE = ½mv²
KE=½(5.97E24kg)(1.12E4 m/s)²
KE=3.7E32 joules

Therefore, the surface escape velocity method yields a minimum energy estimate of 3.7E32 joules. This represents an upper limit for the binding energy of an Earth-like planet, since the escape velocity is not constant. As the outer layers of the planet are blown off, the underlying portions of the planet will have a lower escape velocity. As an aside, the Death Star actually blew Alderaan apart at far greater velocity than necessary, so this figure relates to a minimum-scale planetary explosion, rather than the absurdly rapid explosion we see in the movie.

Method 2: Gravitational Binding Energy- Constant Density

How do we account for the fact that the escape velocity is not constant? To solve this problem, we must resort to Sir Isaac Newton again, and employ calculus (a branch of mathematics in which he was a pioneer). We can use calculus to calculate the gravitational potential energy (and by extension, the escape velocity) not just at the surface, but for all points between the surface and the centre of the planet. By adding up all of these values, we can determine the gravitational binding energy of a planet to a far higher level of accuracy than we achieved with method #1. This process is known as integration, and if you are curious about the basic principles behind it, click here. For a more detailed tutorial on calculus, you may wish to visit Karl's Calculus Tutor which, interestingly enough, happens to touch upon the subject of Alderaan.

In any case, if we refer again to Newton's gravitational potential energy formula:

We can integrate this function from the centre of a planet to its surface, by slicing the planet up into an infinite number of thin "shells". Essentially, we are peeling the planet's skin off layer by layer, like an onion. Each slice has an infinitesimally small thickness, which we shall henceforth refer to as dr. For each slice, we can therefore determine the mass m1 of the slice itself, and the mass m2 of the planet inside the slice:

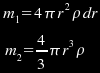
In these formulas, ρ is density (Earth's average density is roughly 5.5E3 kg/m³). The volume of the thin shell is the surface area formula A=4πr² multiplied by the thickness of the shell dr, and we multiply this volume by ρ to get mass m1. The volume of the underlying sphere is the spherical volume formula V=4/3πr³, and we multiply this volume by ρ to get mass m2. Let's suppose we are trying to determine m1 and m2 for a thin shell roughly 2000km deep, so that its radius is roughly 4000km. In this situation, m1 would be 1.1E18dr kg and m2 would be 1.5E24 kg. Now that we have formulas for m1 and m2, we can substitute them into Newton's gravitational potential energy formula and integrate from 0 to r (from the centre to the surface):

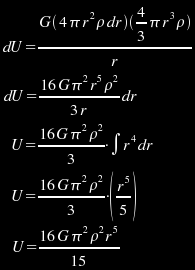
This formula is accurate but over-complicated. It can be substantially simplified by remembering that density is a function of planetary mass and volume, and that volume is a function of radius:

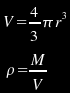
When these equations are substituted into the gravitational binding energy formula, the result is:

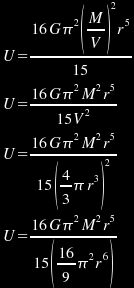
Now, we can easily see that many of the terms in the above formula cancel out, so that the equation simplifies to a much more convenient form:

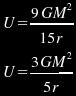
Now, we have a formula for the total binding energy of a planet of uniform density, and all you need is the mass and radius of the planet in question. In the case of Earth, we can easily substitute G=6.6726E-11 m³/(s²·kg), M=5.97E24 kg, and r=6.371E6m to the above formula. The result is 2.2E32 joules, which anyone can independently verify with their own calculations. This represents a lower limit for the gravitational binding energy of a planet, because the density of a planet is not constant; it is always highest in the centre. Therefore, the ratio of mass to volume will increase as the outer layers are "peeled away" rather than staying constant. This will increase the gravitational binding energy.

We have now determined a lower limit (2.2E32 joules) and upper limit (3.7E32 joules) for the gravitational binding energy of an Earth-like planet. If we want to improve the accuracy of our estimates even further, we have to account for the planetary density gradient in the planet, using a third method:

Method 3: Gravitational Binding Energy- Variable Density

A real planet's density is, of course, not uniform. A real planet's density will be extremely high in its core, where the combination of heavy metals and enormous pressure will result in densities in excess of 1E4 kg/m³, and it will drop off in the mantle and crust. In the case of Earth, the density at the surface is perhaps one quarter of the density at the core.

Unfortunately, the only way to incorporate the density gradient into our integration is to perform a curve-fit on the planetary density gradient of an Earth-like planet. This curve fit will result in ρ being a function of r, and it will complicate the integration because we were able to remove the ρ term as a constant from the integration when we were assuming uniform density. Worse yet, the density of a planet is not a nice smooth curve- there are several sharp transitions in the density of a planet, so the integration would have to be broken up into several pieces, each of which deals with a specific density gradient and range of radii.

This is not an insurmountable difficulty of course, but it is nevertheless a significant amount of extra work. Curtis Saxton used planetary density gradients to arrive at the most accurate available figure for the planetary gravitational binding energy of an Earth-like planet in the Star Wars Technical Commentaries, which has been calculated to be about 2.4E32 joules.

Conclusion

Although three different methods are described here (in order of increasing difficulty), they all yield results in the same order of magnitude. The first two methods define upper and lower limits, thus "bracketing" the true figure. The third method is the most ambitious, and attempts to determine where the actual binding energy lies, between the lower and upper limits. All three figures are consistent, and in the same order of magnitude. This demonstrates their accuracy, and the first two methods are simple enough that anyone with a calculator can independently verify the numbers. This information therefore dispels some longstanding notions that it is possible to disrupt a planet without having to supply energy in the range of 1E32 joules. Hopefully, this document will also be somewhat educational, for those who are not already familiar with the machinations behind the numbers and formulae.

Please note that the preceding figures discuss the lower limit, upper limit, and probable value for the gravitational binding energy of a planet. This binding energy is, in turn, the absolute lower limit for the energy that the Death Star must have imparted to Alderaan. However, these figures are extremely conservative because of the speed and violence of the Alderaan explosion. If you are interested in finding out more, visit the Alderaan page.

Addendum

For those who wish to experiment with different values of planetary diameter and surface gravity (I used Earth-like proportions for all of these calculations), a planetary parameter calculator is now available. Click here to experiment with different sizes and gravity strengths, to see what sort of unusual planet you can dream up! Keep in mind that this parameter calculator is intended only for illustrative and educational purposes- in the real universe, there is a typical process of natural planetoid formation that tends to exclude the formation of extreme high-density or low-density planetary bodies. Even gas-giants like Jupiter have average densities in excess of 1000 kg/m³, and planets composed entirely of uranium or some other such high-density element simply do not exist. The page will allow you to experiment with hypothetical planets of virtually any density and size, but you should not fool yourself into thinking that such planets are realistic. Also, you should keep in mind that the Newtonian gravity functions in the page formulae work well for normal planetary bodies but not for extreme conditions like black holes or other super-dense objects.