Kinematics Analysis of Millenium Falcon Turbolaser Impact

in "The Empire Strikes Back"

Written: 1998.08.01

This document represents an attempt to quantify the energy involved in the sudden angular acceleration of the Millenium Falcon after being hit by a turbolaser or laser blast in "The Empire Strikes Back". The basic assumption is that turbolasers use mass-less particles. If the particles in a TL bolt do not carry mass, then their momentum can be calculated using the equations for the momentum of light, and their power levels can be estimated from the kinetic effect upon the Millenium Falcon.

Controlling Equations:

1. The momentum of a laser bolt of any given energy level is p = U/c

2. The moment of inertia for a cylinder rotating about its central diameter is:
   

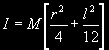
3. The torque necessary to induce a given angular acceleration is T = Ia

4. The torque resultant from an externally applied force is T = Fx

5. The force corresponding to a momentum increase during a known timeframe is F=p/t

Units:

• p = momentum in kg·m/s

• U = energy in J

• c = velocity in m/s

• M = mass in kg

• r = cylinder radius in m

• l = cylinder length in m (in the case of the Falcon this would be its height)

• I = moment of inertia in kg·m²

• T = torque in Nm

• a = angular acceleration in radians/sec² (rotational acceleration in layperson's terms)

• w = angular velocity in radians/sec

• F = force in N

• x = distance from impact point to centre of Falcon

• t = time in seconds

Derivation of Formula:

As per Newton's third law of motion, for every action there is an equal and opposite reaction. Therefore, the reaction torque corresponding to the Falcon's angular acceleration must be equal to the torque applied by the turbolaser:

T₁ = T₂
\ Ia = Fx
F = p/t
\ p = Ia t/x

However, a = w /t and the two time terms refer to the same time element (the angular acceleration must occur in the exact same timeframe as the duration of the turbolaser impact). Therefore, the a t term simplifies to w, and the above equation simplifies to:

p = Iw/x
\ p = U/c
\ U = cIw/x

Estimates for variables

There are no canon figures for the length, width, thickness, and mass of the Millenium Falcon. However, Robert Brown has done extensive work analyzing this famous star freighter in his Falcon web-site at www.synicon.com.au/sw/mf/falcon.htm. I used his figures for the saucer diameter and height of the Falcon:

• Saucer diameter = 27m \ radius r = 13.5m

• Saucer thickness = 6.9m

• From the following snapshot of the precise moment of impact, we can determine the distance from the centre of the Falcon to the turbolaser impact point x = 7m
  

• From the Falcon's size and shape I estimate that its volume is roughly 4000 cubic metres. If we assume that 95% of this volume is air and the remaining material has the density of iron, then the Falcon's mass is approximately 1500 tons. This estimation method makes the Falcon's average density similar to the Enterprise-D's average density according to the Star Trek Technical Manual.

• From the following pair of snapshots (from the start of its rotation to the point where it reaches its maximum angular displacement of 35 degrees in 8 NTSC 0.03-second frames), we can deduce that the angular velocity w = 2.29 rads/s.
  

Calculations

Step 1: Calculate moment of inertia: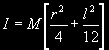

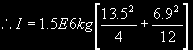
\ I = 7.44E7 kg·m²

Step 2: Calculate turbolaser energy:
U = cIw/x
\ U = 3E8 · 7.44E7 · 2.29 / 7m
\ U = 7.29E15 J = 7290 TJ

Step 3: Compensate for the angle of approach:

We can estimate from the above snapshot that the turbolaser approached at an angle of roughly 30 degrees. This means that the energy estimate must be divided by sin(30°) to account for geometric factors. Therefore, the energy of the TL bolt would be 14580 TJ.

Conclusion

If turbolasers use mass-less particles such as photons (eg. if their operating principle is similar to lasers), and my estimate for the Millenium Falcon's mass is correct, then turbolasers carry approximately 14580 TJ of energy. The turbolaser appears to strike during a single 1/30-second NTSC frame in this sequence, but to be conservative we should assume that the bolt duration is roughly 1/15 seconds. Therefore, the corresponding turbolaser power level is 218700 TW.

As an aside, the rotational kinetic energy of an object is 0.5Iw² at non-relativistic rotational speeds. Therefore, 3.902E8 joules of rotational kinetic energy were added to the Millenium Falcon. However, the physics of collisions involve conservation of linear or angular momentum rather than conservation of kinetic energy, which only happens in elastic collisions.